Υπάρχουν πολυάριθμες μέθοδοι για τον καθορισμό της τάσης ενός οικονομικού εργαλείου. Ίσως η πιο δημοφιλής μέθοδος στην τεχνική ανάλυση είναι αυτή του κινητού μέσου όρου. Επιπλέον, ωστόσο, συχνά χρησιμοποιείται και η μέθοδος της γραμμικής παλινδρόμησης. Επομένως, σήμερα θέλουμε να επεκτείνουμε την εργαλειοθήκη των δεικτών μας με αυτό το εξαιρετικά χρήσιμο εργαλείο.
Στην οικονομετρία και τα χρηματοοικονομικά, η γραμμική παλινδρόμηση - γνωστή και ως μέθοδος των ελαχίστων τετραγώνων (least squares) - είναι απαραίτητη. Η διαδικασία αναπτύχθηκε στα τέλη του 18ου αιώνα από τον μόλις 19 ετών τότε C.F. Gauss. Θα σκιαγραφήσουμε εν συντομία τις βασικές αρχές του υπολογισμού χωρίς να χαθούμε στις λεπτομέρειες. Στη συνέχεια, θα παρουσιάσουμε πρακτικές εφαρμογές.
Στην οικονομετρία και τα χρηματοοικονομικά, η γραμμική παλινδρόμηση - γνωστή και ως μέθοδος των ελαχίστων τετραγώνων (least squares) - είναι απαραίτητη. Η διαδικασία αναπτύχθηκε στα τέλη του 18ου αιώνα από τον μόλις 19 ετών τότε C.F. Gauss. Θα σκιαγραφήσουμε εν συντομία τις βασικές αρχές του υπολογισμού χωρίς να χαθούμε στις λεπτομέρειες. Στη συνέχεια, θα παρουσιάσουμε πρακτικές εφαρμογές.
Τα βασικά
Στον υπολογισμό κινητών μέσων όρων, υπολογίζεται μια μέση αξία για ένα προηγουμένως καθορισμένο μήκος περιόδου. Η γραμμική παλινδρόμηση ακολουθεί διαφορετική οδό. Εδώ υπολογίζεται μια γραμμή για το δεδομένο διάστημα έτσι ώστε να οδηγεί υπολογιστικά ακριβώς μέσω του μέσου των τιμών. Αυτό επιτυγχάνεται με την ελαχιστοποίηση του αθροίσματος των τετραγωνισμένων αποστάσεων των τιμών κλεισίματος στην ευθεία γραμμή. Η μέθοδος υπολογισμού σκιαγραφείται στο διάγραμμα. Συνολικά συνδέσαμε 20 σημεία δεδομένων με μια κυανή γραμμή. Οι αποστάσεις έως τη γραμμή παλινδρόμησης (πράσινη γραμμή) – στην τεχνική ορολογία καλείται και error correction line - σημειώνονται αλφαβητικά με αύξουσα πορεία. Προτού μπορέσουμε να σχεδιάσουμε τη γραμμή παλινδρόμησης, έπρεπε να καθοριστεί η εξίσωση ευθειών γραμμών με μια ρουτίνα βελτιστοποίησης, έτσι ώστε το άθροισμα των τετραγωνισμένων αποκλίσεων a2 + b2 +… + t2 να δίνει ένα ελάχιστο.
Στον υπολογισμό κινητών μέσων όρων, υπολογίζεται μια μέση αξία για ένα προηγουμένως καθορισμένο μήκος περιόδου. Η γραμμική παλινδρόμηση ακολουθεί διαφορετική οδό. Εδώ υπολογίζεται μια γραμμή για το δεδομένο διάστημα έτσι ώστε να οδηγεί υπολογιστικά ακριβώς μέσω του μέσου των τιμών. Αυτό επιτυγχάνεται με την ελαχιστοποίηση του αθροίσματος των τετραγωνισμένων αποστάσεων των τιμών κλεισίματος στην ευθεία γραμμή. Η μέθοδος υπολογισμού σκιαγραφείται στο διάγραμμα. Συνολικά συνδέσαμε 20 σημεία δεδομένων με μια κυανή γραμμή. Οι αποστάσεις έως τη γραμμή παλινδρόμησης (πράσινη γραμμή) – στην τεχνική ορολογία καλείται και error correction line - σημειώνονται αλφαβητικά με αύξουσα πορεία. Προτού μπορέσουμε να σχεδιάσουμε τη γραμμή παλινδρόμησης, έπρεπε να καθοριστεί η εξίσωση ευθειών γραμμών με μια ρουτίνα βελτιστοποίησης, έτσι ώστε το άθροισμα των τετραγωνισμένων αποκλίσεων a2 + b2 +… + t2 να δίνει ένα ελάχιστο.
Στο διάγραμμα 1, η εξίσωση παλινδρόμησης για την πράσινη γραμμή σημειώνεται με πράσινα γράμματα ως y = 0.4331x + 13.253. Αυτό μπορεί να προστεθεί στο πρόγραμμα υπολογιστικών φύλλων (spreadsheet) σε κάθε διάγραμμα μέσω μιας δυνατότητας επιλογής. Με αυτόν τον τύπο μπορούμε να υπολογίσουμε κάθε σημείο στην πράσινη γραμμή παλινδρόμησης. Επιπλέον: Βάσει των γραμμών παλινδρόμησης μπορούμε επίσης να κάνουμε μια πρόβλεψη για το σημείο 21. Ο παράγοντας 0,4331 πριν από τη μεταβλητή x ονομάζεται και κλίση (slope). Αυτή είναι η αξία κατά την οποία θα αυξανόταν η ευθεία γραμμή ανά μονάδα - σε ένα διάγραμμα μετοχών, παραδείγματος χάριν, μια ημέρα.
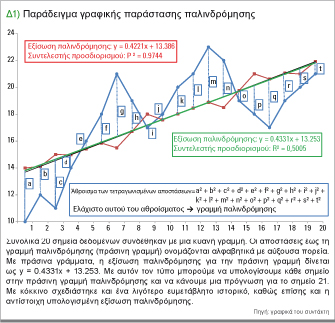
Με τη βοήθεια του σκίτσου στο διάγραμμα 1 γίνεται αμέσως σαφές ότι μια γραμμή παλινδρόμησης μπορεί να προσαρμοστεί ακριβέστερα στις τιμές καθώς το εύρος της διακύμανσης είναι μικρότερο. Το βέλτιστο θα ήταν να είχαμε όλες τις πορείες σε ευθεία γραμμή. Αλλά αυτό σχεδόν ποτέ δεν θα είναι εφικτό. Κατά συνέπεια, σχεδιάσαμε μια λιγότερο ευμετάβλητη τάση (κόκκινη γραμμή) στο διάγραμμα. Όπως μπορείτε να δείτε, η εξίσωση ευθειών γραμμών της πράσινης γραμμής από το πρώτο παράδειγμα είναι πολύ παρόμοια. Ωστόσο, υπάρχει μια κρίσιμη διαφορά. Κάτω από την εξίσωση ευθειών γραμμών, η αξία για το συντελεστή προσδιορισμού δίνεται τώρα ως 0,9744. Προηγουμένως, ήταν ακόμα ίση με 0,5005. Ο συντελεστής προσδιορισμού (γνωστός και ως R-square) είναι ένα κριτήριο για την παλινδρόμηση και μπορεί να έχει τιμές μεταξύ 0 και 1. Σε αυτήν την περίπτωση βρίσκεται πιο κοντά στο 1, όσο μικρότερη είναι η κατανομή των μονάδων γύρω από τη γραμμή παλινδρόμησης.
Σύγκριση με τους κινητούς μέσους όρους
Σύμφωνα με αυτήν την εισαγωγική θεωρία, ας συγκρίνουμε τη γραμμική παλινδρόμηση με τους κινητούς μέσους όρους. Για αυτόν το σκοπό είναι απαραίτητο ένα σχόλιο για την επιλογή του μήκους της περιόδου. Οι στατιστικοί υπολογισμοί υπόκεινται πάντα σε έναν βαθμό αβεβαιότητας. Η αβεβαιότητα αυξάνεται, όταν μειώνεται ο αριθμός των διαθέσιμων δεδομένων για τις μονάδες. Ο βασικός τύπος είναι ότι το λάθος είναι ανάλογο προς το 1/ root (n), όπου το n είναι το μήκος της περιόδου. Για ένα μήκος περιόδου ίσο με δέκα, πρέπει επομένως να αναμένουμε μια μέτρηση λάθους ίση με 1 / root (10) = 31 τοις εκατό. Για μήκος περιόδου ίσο με 100, το λάθος είναι μόνο 10 τοις εκατό. Στο ακόλουθο παράδειγμα, έχουμε επιλέξει μια περίοδο 30 ημερών εκτέλεσης συναλλαγών. Αυτό αντιστοιχεί σε μια περίοδο έξι εβδομάδων.
Σύμφωνα με αυτήν την εισαγωγική θεωρία, ας συγκρίνουμε τη γραμμική παλινδρόμηση με τους κινητούς μέσους όρους. Για αυτόν το σκοπό είναι απαραίτητο ένα σχόλιο για την επιλογή του μήκους της περιόδου. Οι στατιστικοί υπολογισμοί υπόκεινται πάντα σε έναν βαθμό αβεβαιότητας. Η αβεβαιότητα αυξάνεται, όταν μειώνεται ο αριθμός των διαθέσιμων δεδομένων για τις μονάδες. Ο βασικός τύπος είναι ότι το λάθος είναι ανάλογο προς το 1/ root (n), όπου το n είναι το μήκος της περιόδου. Για ένα μήκος περιόδου ίσο με δέκα, πρέπει επομένως να αναμένουμε μια μέτρηση λάθους ίση με 1 / root (10) = 31 τοις εκατό. Για μήκος περιόδου ίσο με 100, το λάθος είναι μόνο 10 τοις εκατό. Στο ακόλουθο παράδειγμα, έχουμε επιλέξει μια περίοδο 30 ημερών εκτέλεσης συναλλαγών. Αυτό αντιστοιχεί σε μια περίοδο έξι εβδομάδων.
Παράδειγμα
Το διάγραμμα 2 παρουσιάζει τον DAX με τον δείκτη προοδευτικής παλινδρόμησης. Για σύγκριση, προσθέσαμε έναν κινητό μέσο όρο. Το μήκος περιόδου είναι 30 ημέρες και για τους δύο δείκτες. Είναι σαφές ότι η χρονική υστέρηση της γραμμής παλινδρόμησης είναι πολύ μικρή. Αυτό είναι επίσης σωστό επειδή η γραμμή παλινδρόμησης διαμορφώνεται κατά τέτοιο τρόπο ώστε τα σημεία των δεδομένων γύρω από αυτήν την γραμμή παρουσιάζουν διακυμάνσεις. Είναι επίσης εντυπωσιακό ότι η γραμμή παλινδρόμησης υποδεικνύει μια αλλαγή τάσης πολύ πιο γρήγορα από έναν κινητό μέσο όρο με το ίδιο μήκος περιόδου. Ωστόσο, όπως συμβαίνει με οποιοδήποτε δείκτη παρακολούθησης τάσης, η παλινδρόμηση έχει το μειονέκτημα να μην παρέχει χρήσιμα αποτελέσματα σε ευμετάβλητες πλάγιες μετακινήσεις.
Το διάγραμμα 2 παρουσιάζει τον DAX με τον δείκτη προοδευτικής παλινδρόμησης. Για σύγκριση, προσθέσαμε έναν κινητό μέσο όρο. Το μήκος περιόδου είναι 30 ημέρες και για τους δύο δείκτες. Είναι σαφές ότι η χρονική υστέρηση της γραμμής παλινδρόμησης είναι πολύ μικρή. Αυτό είναι επίσης σωστό επειδή η γραμμή παλινδρόμησης διαμορφώνεται κατά τέτοιο τρόπο ώστε τα σημεία των δεδομένων γύρω από αυτήν την γραμμή παρουσιάζουν διακυμάνσεις. Είναι επίσης εντυπωσιακό ότι η γραμμή παλινδρόμησης υποδεικνύει μια αλλαγή τάσης πολύ πιο γρήγορα από έναν κινητό μέσο όρο με το ίδιο μήκος περιόδου. Ωστόσο, όπως συμβαίνει με οποιοδήποτε δείκτη παρακολούθησης τάσης, η παλινδρόμηση έχει το μειονέκτημα να μην παρέχει χρήσιμα αποτελέσματα σε ευμετάβλητες πλάγιες μετακινήσεις.
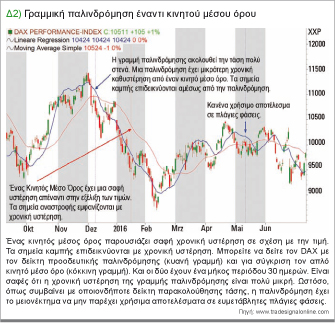
Το διάγραμμα δείχνει ότι αυτό ισχύει για την περίοδο από τον Απρίλιο μέχρι τον Ιούνιο του 2016. Ως προσωρινό συμπέρασμα, μπορούμε να πούμε ότι η γραμμή παλινδρόμησης είναι στενά συνδεδεμένη με την τάση της τιμής σε φάσεις με τάση. Ωστόσο, πρέπει να είναι δύσκολο να χρησιμοποιηθούν αυτές και μόνο οι πληροφορίες. Με την κλίση της γραμμής παλινδρόμησης και την μέτρηση ποιότητας έχουμε δυο επιπλέον πληροφορίες που μπορούμε να χρησιμοποιήσουμε για να αξιολογήσουμε την τάση.
Συνυπολογισμός της κλίσης και της ποιότητας
Για αυτόν το σκοπό επεκτείναμε το διάγραμμα με αυτούς τους δύο δείκτες στο διάγραμμα 3. Η κλίση (hr RegSlope - κόκκινη γραμμή) σχεδιάζεται ακριβώς κάτω από το διάγραμμα και ο συντελεστής προσδιορισμού (hr R-square πράσινη γραμμή) σχεδιάζεται από κάτω. Η ιδέα είναι η ακόλουθη: Μια ανοδική τάση ξεκινάει συνήθως μετά από μια καθοδική τάση ή μετά από μια πλάγια μετακίνηση. Και στις δύο περιπτώσεις, η ποιότητα της τάσης είναι αρχικά χαμηλή. Η αξία του συντελεστή καθορισμού πρέπει επομένως να είναι επίσης αρκετά μικρή.
Για αυτόν το σκοπό επεκτείναμε το διάγραμμα με αυτούς τους δύο δείκτες στο διάγραμμα 3. Η κλίση (hr RegSlope - κόκκινη γραμμή) σχεδιάζεται ακριβώς κάτω από το διάγραμμα και ο συντελεστής προσδιορισμού (hr R-square πράσινη γραμμή) σχεδιάζεται από κάτω. Η ιδέα είναι η ακόλουθη: Μια ανοδική τάση ξεκινάει συνήθως μετά από μια καθοδική τάση ή μετά από μια πλάγια μετακίνηση. Και στις δύο περιπτώσεις, η ποιότητα της τάσης είναι αρχικά χαμηλή. Η αξία του συντελεστή καθορισμού πρέπει επομένως να είναι επίσης αρκετά μικρή.
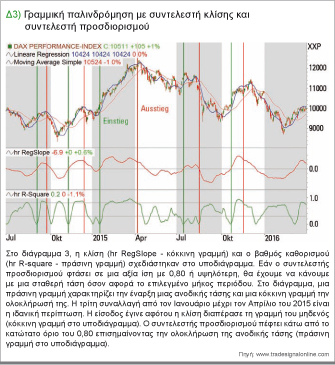
Το κατώτατο όριο είναι 0,30. Εάν ξεκινήσει μια νέα ανοδική τάση, η κλίση της παλινδρόμησης είναι θετική. Κατά συνέπεια, έχουμε δύο κριτήρια για την έναρξη μιας ανοδικής τάσης: μια κλίση μεγαλύτερη από μηδέν και έναν συντελεστή καθορισμού κάτω από 0,30. Εάν αναπτυχθεί μια σταθερή ανοδική τάση, χαρακτηρίζεται από μια θετική κλίση και ένα αυξανόμενο R-square.
Εάν ο συντελεστής προσδιορισμού φτάσει σε μια αξία ίση με 0,80 ή υψηλότερη θα έχουμε να κάνουμε με μια σταθερή τάση όσον αφορά το επιλεγμένο μήκος περιόδου. Εάν η αξία μειωθεί στη συνέχεια κάτω από αυτό το κατώτατο όριο, υπάρχει μεγάλη πιθανότητα να έχει ολοκληρωθεί και πάλι η τάση. Ακολουθώντας αυτούς τους κανόνες, έχουμε σημειώσει την αρχή και το τέλος των ανοδικών τάσεων με κατακόρυφες γραμμές στο διάγραμμα. Μια πράσινη γραμμή χαρακτηρίζει την έναρξη μιας ανοδικής τάσης και μια κόκκινη γραμμή την ολοκλήρωσή της. Η τρίτη συναλλαγή μεταξύ του Ιανουαρίου και του Απριλίου 2015 είναι η ιδανική περίπτωση. Η είσοδος πραγματοποιήθηκε αφότου η κλίση είχε ανέβει πάνω από τη γραμμή του μηδενός (κόκκινη γραμμή στο υποδιάγραμμα). Ο συντελεστής προσδιορισμού πέφτει κάτω από το κατώτατο όριο του 0,80, σηματοδοτώντας την ολοκλήρωση της ανοδικής τάσης (πράσινη γραμμή στο υποδιάγραμμα).
Με το επόμενο σήμα τον Ιούλιο του 2015, ο συντελεστής προσδιορισμού παραμένει σε ένα πολύ χαμηλό επίπεδο. Σε αυτήν την περίπτωση, μια μειωμένη κλίση κάτω από το μηδέν υποδεικνύει το τέλος της ανοδικής μετακίνησης. Με τους απλούς κανόνες που περιγράφονται, το διάγραμμα παρουσιάζει πέντε ανοδικές τάσεις μεταξύ του Αυγούστου 2014 και Ιουλίου 2015. Οι τέσσερις ενδείξεις θα ήταν επιτυχείς. Δεν είναι κακό το αποτέλεσμα για ένα σχετικά απλό σύνολο κανόνων.
Συμπέρασμα
Η χρήση της παλινδρόμησης παραμελείται στην τεχνική ανάλυση λανθασμένα. Ενδεχομένως να τρομάζει αρχικά ο κάπως υψηλότερος μαθηματικός κόπος που απαιτείται. Αλλά για αυτό υπάρχουν υπολογιστές. Ως υποπροϊόντα, μας παρέχονται δύο χρήσιμοι αρωγοί: η κλίση της τάσης και η ποιότητα της παλινδρόμησης. Η τελευταία κυρίως αξία είναι αυξημένου ενδιαφέροντος. Αυτές οι λειτουργίες είναι διαθέσιμες ως κώδικας ανοικτής πηγής σε κάθε λογισμικό διαγραμμάτων. Μια επέκταση της παρουσιαζόμενης μεθόδου θα ήταν η πρόσθετη αλληλεπίδραση των τιμών παλινδρόμησης για διαφορετικούς χρονικούς ορίζοντες.
Η χρήση της παλινδρόμησης παραμελείται στην τεχνική ανάλυση λανθασμένα. Ενδεχομένως να τρομάζει αρχικά ο κάπως υψηλότερος μαθηματικός κόπος που απαιτείται. Αλλά για αυτό υπάρχουν υπολογιστές. Ως υποπροϊόντα, μας παρέχονται δύο χρήσιμοι αρωγοί: η κλίση της τάσης και η ποιότητα της παλινδρόμησης. Η τελευταία κυρίως αξία είναι αυξημένου ενδιαφέροντος. Αυτές οι λειτουργίες είναι διαθέσιμες ως κώδικας ανοικτής πηγής σε κάθε λογισμικό διαγραμμάτων. Μια επέκταση της παρουσιαζόμενης μεθόδου θα ήταν η πρόσθετη αλληλεπίδραση των τιμών παλινδρόμησης για διαφορετικούς χρονικούς ορίζοντες.
Αυτό θα μπορούσε στη συνέχεια να χρησιμοποιηθεί για να δώσει στοιχεία για τη σταθερότητα της συμπεριφοράς της τρέχουσας τάσης ως λειτουργία της χρονικής διάρκειας. Δεν υπάρχουν όρια στον πειραματισμό.

stocklearning.gr

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου